ronkathon

Overview

Ronkathon is a collection of cryptographic primitives implemented in Rust. It is inspired by the python plonkathon repository and plonk-by-hand. We use the same curve and field as plonk-by-hand (which is not secure) and the goal of this repository is to work towards building everything from scratch to understand everything from first principles.

Multivariate polynomials and sum-check

This project implements the sum-check protocol for multivariate polynomials over finite fields. The sum-check protocol is an interactive proof system where a prover convinces a verifier of the sum of a multivariate polynomial over a boolean hypercube. This implementation includes:

• A MultiVarPolynomial struct which represents a multivariate polynomial
• A SumCheckProver for generating proofs
• A SumCheckVerifier for verifying proofs
• A SumCheck struct that encapsulates the entire protocol.

You can use:

cargo run --example sumcheck_ex

to run example code.

Primitives

• Fundamental Algebraic Structures
  • Group
  • Fields and Their Extensions
    • Binary Fields
• Curves and Their Pairings
• Polynomials
• KZG Commitments
• Reed-Solomon Codes
• Merkle Proofs
• DSL

Signatures

• Digital Signature Algorithms
  • Elliptic Curve Digital Signature Algorithm(ECDSA)
  • Edwards-Curve Digital Signature Algorithm(EdDSA)

Encryption

Asymmetric

• RSA

Symmetric

• Ciphers:

  • DES
  • AES
  • ChaCha

• Modes of Operation

  • ECB, CBC, CTR, GCM

Hash

• Sha256 Hash
• Poseidon Hash

Resources

We have found the following resources helpful in understanding the foundational mathematics behind this implementation. After going through these, you should be able to understand the codebase

Theoretic Resources

• Plonk by Hand P1
• Plonk by Hand P2
• Plonk by Hand P3

Code References

• Plonkathon
• Plonky3
• py_pairing
• arkworks

Math

To see computations used in the background, go to the math/ directory. From there, you can run the .sage files in a SageMath environment. In particular, the math/field.sage computes roots of unity in the PlutoField which is of size 101. To install sage on your machine, follow the instructions here. If you are on a Mac, you can install it via homebrew with brew install --cask sage.

Building mdBook

To locally build/serve the mdBook site, install mdBook and mdbook-katex:

cargo install mdbook
cargo install mdbook-katex

To build, run:

cargo run --bin create_mdbook
cp -r assets book/
mdbook build

If you want to serve locally, run mdbook serve.

License

Licensed under the Apache License, Version 2.0 (LICENSE-APACHE or http://www.apache.org/licenses/LICENSE-2.0)

Contributing

We welcome contributions to our open-source projects. If you want to contribute or follow along with contributor discussions, join our main Telegram channel to chat about Pluto's development.

Our contributor guidelines can be found at CONTRIBUTING.md. A good starting point is issues labelled 'bounty' in our repositories.

Unless you explicitly state otherwise, any contribution intentionally submitted for inclusion in the work by you, as defined in the Apache-2.0 license, shall be licensed as above, without any additional terms or conditions.

Algebra

Groups $G$ are algebraic structures which are set and has a binary operation $\cdot$ that combines two elements $a,b$ of the set to produce a third element $a\cdot b$ in the set. The operation is said to have following properties:

1. Closure: $a\cdot b=c\in G$
2. Associative: $(a\cdot b)\cdot c=a\cdot (b\cdot c)$
3. Existence of Identity element: $a\cdot 0=0\cdot a=a$
4. Existence of inverse element for every element of the set: $a\cdot b=0$
5. Commutativity: Groups which satisfy an additional property: commutativity on the set of elements are known as Abelian groups, $a\cdot b=b\cdot a$.

Examples:

• $Z$ is a group under addition defined as $(Z,+)$
• $(Z/nZ{)}^{\times }$ is a finite group under multiplication
• Equilateral triangles for a non-abelian group of order 6 under symmetry.
• Invertible $n\times n$ form a non-abelian group under multiplication.

Rings are algebraic structures with two binary operations $R(+,\cdot )$ satisfying the following properties:

1. Abelian group under +
2. Monoid under $\cdot$
3. Distributive with respect to $\cdot$

Examples:

• $Z/nZ$ form a ring
• a polynomial with integer coefficients: $Z[x]$ satisfy ring axioms

Fields are algebraic structures with two binary operations $F(+,\cdot )$ such that:

• Abelian group under $+$
• Non-zero numbers $F-\{0\}$ form abelian group under $\cdot$
• Multiplicative distribution over $+$

Fields can also be defined as commutative ring $(R,+,\cdot )$ with existence of inverse under $\cdot$. Thus, every Field can be classified as Ring.

Examples:

• $\mathbb{Q},\mathbb{R},\mathbb{C}$, i.e. set of rational, real and complex numbers are all Fields.
• $\mathbb{Z}$ is not a field.
• $Z/nZ$ form a finite field under modulo addition and multiplication.

Finite fields are field with a finite order and are instrumental in cryptographic systems. They are used in elliptic curve cryptography, RSA, and many other cryptographic systems. This module provides a generic implementation of finite fields via two traits and two structs. It is designed to be easy to use and understand, and to be flexible enough to extend yourself.

Constant (Compile Time) Implementations

Note that traits defined in this module are tagged with #[const_trait] which implies that each method and associated constant is implemented at compile time. This is done purposefully as it allows for generic implementations of these fields to be constructed when you compile ronkathon rather than computed at runtime. In principle, this means the code runs faster, but will compile slower, but the tradeoff is that the cryptographic system is faster and extensible.

Field

Traits

• FiniteField: a field $({\mathbb{F}}_p,+,\cdot )$ where $p$ is a prime number.
• ExtensionField: an extension of a field $({\mathbb{F}}_{p^k},+,\cdot )$ where $p$ is a prime number and ${\mathbb{F}}_{p^k}$ is an extension of ${\mathbb{F}}_p$.

The two traits used in this module are FiniteField and ExtensionField which are located in the field and field::extension modules respectively. These traits are interfacial components that provide the necessary functionality for field-like objects to adhere to to be used in cryptographic systems.

FiniteField

The FiniteField trait is used to define a finite field in general. The trait itself mostly requires functionality from traits in the Rust core::ops module such as Add, Sub, Mul, and Div (and their corresponding assignment, iterator, and related operations). In effect, these constraints provide us the algebraic structure of a field.

A bit more specifically, the FiniteField trait requires the following associated constants and (const) methods:

• const ORDER: Self - The order of the field.
• const ZERO: Self - The additive identity.
• const ONE: Self - The multiplicative identity.
• const PRIMITIVE_ELEMENT: Self - A primitive element of the field, that is, a generator of the multiplicative subgroup of the field.
• inverse(&self) -> Option<Self> - The multiplicative inverse of a nonzero field element. Returns None if the element is zero.
• pow(&self, power: usize) -> Self - Multiply a field element by itself power times.
• primitive_root_of_unity(n: usize) -> Self - The primitive $n$th root of unity of the field.

ExtensionField

The ExtensionField trait is used to define an extension field of a finite field. It inherits from the FiniteField trait and enforces that algebraic operations from the base field are implemented. It is generic over the prime P of the underlying base field as well as the degree N of the extension intended. The only additional constraint aside from the FiniteField trait and adherence to algebraic operations on the base field is:

• const IRREDUCIBLE_POLYNOMIAL_COEFFICIENTS: [PrimeField<P>; N + 1] - The coefficients of the irreducible polynomial that defines the extension field.

We will discuss PrimeField<P> momentarily.

Structs

The structs that implement these traits are

• PrimeField
• GaloisField

[!NOTE] In principal, PrimeField and GaloisField could be combined into just GaloisField but are separated for clarity at the moment. These structs are both generic over the prime P of the field, but GaloisField is also generic over the degree N of the extension field.

PrimeField

The PrimeField struct is a wrapper around a usize by:

#![allow(unused)]
fn main() {
pub struct PrimeField<const P: usize> {
    value: usize,
}
}

that implements the FiniteField trait and has some compile-time constructions. For example, upon creation of an element of PrimeField<P> we utilize the const fn is_prime<const P: usize>() function which will panic! if P is not prime. Hence, it is impossible to compile a program for which you construct PrimeField<P> where P is not prime.

Furthermore, it is possible to determine the PRIMITIVE_ELEMENT of the field at compile time so that we may implement FiniteField for any prime P without any runtime overhead. The means to do so is done in the field::prime::find_primitive_element function which is a brute force search for a primitive element of the field that occurs as Rust compiles ronkathon.

All of the relevant arithmetic operations for PrimeField<P> are implemented in field::prime::arithmetic.

GaloisField

The GaloisField struct is a wrapper around a PrimeField<P> by:

#![allow(unused)]
fn main() {
use ronkathon::algebra::field::prime::PrimeField;
pub struct GaloisField<const N: usize, const P: usize> {
    value: [PrimeField<P>; N],
}
}

where the [PrimeField<P>; N] is the representation of the field element as coefficients to a polynomial in the base field modulo the irreducible polynomial of the extension field (recall the ExtensionField trait above specifies the need for an irreducible polynomial).

We implement ExtensionField for specific instances of GaloisField<N, P> as, at the moment, we do not have a general compile-time-based implementation of extension fields as we do with PrimeField<P>, though it is possible to do so. Instead, we have implemented much of the arithmetic operations for GaloisField<N, P> in field::extension::arithmetic, but left some that needs to be computed by hand for the user to implement (for now). See, for instance, field::extension::gf_101_2 implements the IRREDUCIBLE_POLYNOMIAL_COEFFICIENTS for GaloisField<2, 101> as well as the remaining arithmetic operations. There is a method to compute both the IRREDUCIBLE_POLYNOMIAL_COEFFICIENTS at compile time as well as the PRIMITIVE_ELEMENT of the field, but it is not implemented at the moment.

Binary Fields

Binary fields denoted as $GF(2)=Z/2Z$, i.e. quotient ring of integers modulo ring of 2 integers $\{0,1\}$, are a special class of Finite Fields, with modulus = $2$. Main properties exhibited by Binary fields are:

• Addition corresponds to bitwise XOR
• Multiplication corresponds to bitwise AND
• since, $x+x=0⟹x=-x$, i.e. negation of a number is itself

This allows for extremely efficient arithmetic that is much more hardware friendly than fields based on other primes.

Binary Extension fields

Finite field with $2^k$ elements represented as $GF(2^k)=F(2)[X]/f(X)$, where $f(X)$ is an irreducible of degree $k$. Used extensively in cryptography like AES block cipher and error-correcting codes.

Two ways of representing $GF(2^k)$:

• univariate basis - two ways of representing in univariate basis as well, namely:
  • polynomial basis: elements are represented as degree k-1 polynomial $A_{k-1}{\alpha }^{k-1}+\cdots +A_1\alpha +A_0$ by equivalence class $GF(2)/f(x)$, where f(x) is any irreducible in the kth power.
  • normal basis: elements are represented as taking powers of an element from the field
• multilinear basis: there’s one other way of representing elements, i.e. Multilinear basis, where elements are represented by monomials: $1,X_0,X_1\cdot X_0,X_2\cdot X_1\cdot X_0,\dots ,X_0\dots X_{l-1}$, with each coefficient in $GF(2)$.

Extension field using towers

Binius realises binary extension field using towers formalised in Weidemann et al..

Basic idea is to derive sequence of polynomial rings inductively

• start with ${\tau }_0={\mathbb{F}}_2=\{0,1\}$
• set ${\tau }_1={\tau }_0[X_0]/(X_0^2+X_0+1)={\mathbb{F}}_{2^2}$, namely $\{0,1,X_0,1+X_0\}$.
• set ${\tau }_2={\tau }_1[X_1]/(X_1^2+X_0{X}_1+1)={\mathbb{F}}_{2^{2^2}}$
• continue this further with ${\tau }_0\subset {\tau }_1\subset \cdots \subset {\tau }_{i-1}\subset {\tau }_i={\tau }_{i-1}[X_{i-1}]/f_{i-1}(X_{i-1})$, where $f_{i-1}(X_{i-1})=X_{i-1}^2+X_{i-1}{X}_{i-2}+1$ is an irreducible in ${\tau }_i$

In practice, Extension Field elements are represented in vector of binary field $G{F}_2$ components of length $2^K$. Forms a multilinear basis of the form ${\beta }_v={\prod }_{i=0}^{K-1}(v_i{X}_i+(1-v_i))$, where $v_i=\{0,1\}$.

Let's take an example of K=2, this forms a field extension of $GF(2^{2^2})=GF(2^4)$. Let's form our basis vector, with $v=\{0,1,2,3\}$:

• $v=0$: representing in binary form, $v=\{0,0\}$, ${\beta }_v={\prod }_{i=0}^{k-1}(0\cdot X_i+(1-0))=1$
• $v=1=\{0,1\}⟹{\beta }_v=X_0$
• $v=\{1,0\}⟹{\beta }_v=X_1$
• $v=\{1,1\}⟹{\beta }_v=X_0{X}_1$

Now, we have our basis to represents numbers in $GF(2^4)$, taking few examples:

• $10=\{1,0,1,0\}⟹X_0+X_0{X}_1$
• $7=\{0,1,1,1\}⟹1+X_0+X_1$

A very nice property of binary fields is defining an element using it's subfield, using it's first and second halves in the subfield: $a=a_0+a_1{X}_{i-1}$

Arithmetic in Binary Extensions

• Addition, Subtraction is just bitwise XOR
• Negation is the element itself
• Multiplication is done using a hybrid of Karatsuba multiplication
• Inversion is $x^{(p-2)}$, using Fermat's little theorem

Group

Traits

• Group: a generic group $(G,\cdot )$ where $G$ is a set and $\cdot$ is a binary operation.
• FiniteGroup: a group with finite elements defined using Finite trait
• AbelianGroup: group with commutative operation
• FiniteCyclicGroup: a finite group with a generator.

Group

Group represents a group with finite elements. It defines a binary operation on the set of elements of the group.

• IDENTITY: The identity element of the group.
• inverse(&self) -> Self: inverse of the element.
• operation(a: &Self, b: &Self) -> Self: the operation of the group.
• scalar_mul(&self, scalar: &Self::Scalar): multiplication of the element by a scalar.

Structs

The structs that implement these traits are

• MultiplicativePrimeGroup

MultiplicativePrimeGroup

The MultiplicativePrimeGroup struct is a wrapper around a usize that defines $(Z/nZ{)}^{\ast }$ for a prime power $n=p^k$ with binary operation as $\times$:

#![allow(unused)]
fn main() {
pub struct MultiplicativePrimeGroup<const P: usize, const K: usize>(usize);
}

It uses compile time assertions to check that $P$ is prime.

Examples

Symmetric Group example showcases how Group trait is implemented for any struct.

Codes

In some cryptographic protocols, we need to do encoding and decoding. Specifically, we implement the Reed-Solomon encoding and decoding in this module.

Reed-Solomon Encoding

The Reed-Solomon encoding is a kind of error-correcting code that works by oversampling the input data and adding redundant symbols to the input data. Our specific case takes a Message<K, P> that is a list of K field elements for the PrimeField<P>. We can then call the encode::<N>() method on the Message<K, P> to get a Codeword<N, K, P> that is an encoded version of message with redundancy added.

First, we create a polynomial in Monomial form from our message by having each element of the message be a coefficient of the polynomial. To do this encoding, we get the Nth root of unity in the field and evaluate the polynomial at each of the powers of that root of unity. We then store these evaluations in the codeword along with the point at which they were evaluated. In effect, this is putting polynomial into the Lagrange basis where the node points are the Nth roots of unity.

That is to say, we have a message $M=(m_0,m_1,\dots ,m_{K-1})$ and we encode it into a codeword $C=(c_0,c_1,\dots ,c_{N-1})$ where: $$\begin{array}{rl}{c}_i& =\sum _{j=0}^{K-1}{m}_j\cdot {\omega }^{ij}\end{array}$$ where $\omega$ is the Nth root of unity.

Reed-Solomon Decoding

Given we have a Codeword<M, K, P>, we can call the decode() method to get a Message<K, P> that is the original message so long as the assertion M>=N holds. Doing the decoding now just requires us to go from the Lagrange basis back to the monomial basis. For example, for a degree 2 polynomial, we have: $$\begin{array}{rl}{\ell }_0(x)& =\frac{(x-\omega )(x-{\omega }^2)}{(1-\omega )(1-{\omega }^2)}\\ {\ell }_1(x)& =\frac{(x-1)(x-{\omega }^2)}{(\omega -1)(\omega -{\omega }^2)}\\ {\ell }_2(x)& =\frac{(x-1)(x-\omega )}{({\omega }^2-1)({\omega }^2-\omega )}\end{array}$$ where ${\ell }_i(x)$ is the $i$th Lagrange basis polynomial.

Effectively, we just need to expand out our codeword in this basis and collect terms: $$\begin{array}{rl}{c}_0{\ell }_0(x)+c_1{\ell }_1(x)+c_2{\ell }_2(x)& =m_0+m_{1}x+m_2{x}^2\end{array}$$ where $m_i$ are the coefficients of the original message. Note that we can pick any N points of the codeword to do this expansion, but we need at least K points to get the original message back. For now, we just assume the code is the same length for the example.

Multiplying out the left hand side we get the constant coefficient as: $$\begin{array}{r}{m}_0=\frac{c_0\omega {\omega }^2}{(\omega -1)({\omega }^2-1)}+\frac{c_1(1){\omega }^2}{(1-\omega )({\omega }^2-\omega )}+\frac{c_2(1)\omega }{(1-{\omega }^2)(\omega -{\omega }^2)}\end{array}$$ the linear coefficient as: $$\begin{array}{r}-m_1=\frac{c_0(\omega +{\omega }^2)}{(\omega -1)({\omega }^2-1)}+\frac{c_1(1+{\omega }^2)}{(1-\omega )({\omega }^2-\omega )}+\frac{c_2(1+\omega )}{(1-{\omega }^2)(\omega -{\omega }^2)}\end{array}$$ the quadratic coefficient as: $$\begin{array}{r}{m}_2=\frac{c_0}{(\omega -1)({\omega }^2-1)}+\frac{c_1}{(1-\omega )({\omega }^2-\omega )}+\frac{c_2}{(1-{\omega }^2)(\omega -{\omega }^2)}\end{array}$$

This process was generalized in the decode() method.

DSL

introduces a simple DSL, originally from 0xPARC's Plonkathon, for writing circuits that can be compiled to polynomials specific to PLONK prover's algorithm.

let's take an example to compute $x^3+x+5$:

x public
x2 <== x * x
out <== x2 * x + 5

Each line of DSL is a separate constraint. It's parsed and converted to corresponding WireValues, i.e. variables and coefficients for each wire. Vanilla PLONK supports fan-in 2 arithmetic (add and mul) gates, so each constraint can only support a maximum of 1 output and 2 distinct input variables with numeric constants.

Parser rules

• supports <== for assignment and === for arithmetic equality checks
• mark variables as public in the beginning of the program.
• only supports quadratic constraints, i.e. don't support y <== x * x * x.
• each token should be separated by space.

Outputs parsed output in form of WireCoeffs values and coefficients.

• wires: represent variables corresponding to gate wires in each constraint.
• coefficients: coefficient corresponding to each variable.

#![allow(unused)]
fn main() {
/// Values of wires with coefficients of each wire name
#[derive(Debug, PartialEq)]
pub struct WireCoeffs<'a> {
  /// variable used in each wire
  pub wires:  Vec<Option<&'a str>>,
  /// coefficients of variables in wires and [`Gate`]
  pub coeffs: HashMap<String, i32>,
}
}

Example parser outputs

• x public => (['x', None, None], {'$public': 1, 'x': -1, '$output_coeffs': 0}
• b <== a * c => (['a', 'c', 'b'], {'a*c': 1})
• d <== a * c - 45 * a + 987 => (['a', 'c', 'd'], {'a*c': 1, 'a': -45, '$constant': 987})

Some default coefficients are used for certain constraints:

• $constant: for constant variables
• $output_coeffs: for output variables. Example: -a <== b * b has $output_coeffs as -1
• $public: for public variable declarations

Our example wire values gets parsed as:

• x public => ['x', None, None], {'$public': 1, 'x': -1, '$output_coeffs': 0}
• x2 <== x * x => ['x', 'x', 'x2'], {'x*x': 1}
• out <== x2 * x + 5 => ['x2', 'x', 'out'], {'x2*x': 1, '$constant': 5}

Gate

Gate represents the values corresponding to each wire in a gate:

flowchart BT
l[left input]-->a((x))
r[right input]-->a
a-->o[output=l*r]

l2[left input]-->b((+))
r2[right input]-->b
b-->o2[output=l+r]

#![allow(unused)]
fn main() {
/// Fan-in 2 Gate representing a constraint in the computation.
/// Each constraint satisfies PLONK's arithmetic equation: `a(X)QL(X) + b(X)QR(X) + a(X)b(X)QM(X) +
/// o(X)QO(X) + QC(X) = 0`.
pub struct Gate {
  /// left wire value
  pub l: PlutoScalarField,
  /// right wire value
  pub r: PlutoScalarField,
  /// output wire, represented as `$output_coeffs` in wire coefficients
  pub o: PlutoScalarField,
  /// multiplication wire
  pub m: PlutoScalarField,
  /// constant wire, represented as `$constant` in coefficients
  pub c: PlutoScalarField,
}
}

Taking our example:

• x public => ['x', None, None], {'$public': 1, 'x': -1, '$output_coeffs': 0}
  • gate values are: {'l': 1, 'r': 0, 'o': 0, 'c': 0, 'm': 0}
• x2 <== x * x => ['x', 'x', 'x2'], {'x*x': 1}
  • gate values: {'l': 0, 'r': 0, 'm': -1, 'o': 1, 'c': 0}
• out <== x2 * x + 5 => ['x2', 'x', 'out'], {'x2*x': 1, '$constant': 5}
  • gate values: {'l': 0, 'r': 0, 'm': -1, 'o': 1, 'c': 5}

Program

Creates a program from the parsed DSL output containing required polynomials used for PLONK proving step.

Converts WireValues to required polynomials in PLONK, i.e.

• Preprocessed polynomials:
  • selector polynomials: $[Q_L,Q_R,Q_M,Q_O,Q_C]$
  • permutation helpers: $[S_1,S_2,S_3]$

To get selector polynomials from constraints, each constraint is parsed into fan-in 2 arithmetic gates as explained above and wire values are assigned to respective wires in lagrange form.

#![allow(unused)]
fn main() {
/// `CommonPreprocessedInput` represents circuit related input which is apriori known to `Prover`
/// and `Verifier` involved in the process.
pub struct CommonPreprocessedInput {
  /// multiplicative group order
  pub group_order: usize,
  /// Q_L(X): left wire selector polynomial
  pub ql:          Poly,
  /// Q_R(X): right wire selector polynomial
  pub qr:          Poly,
  /// Q_M(X): multiplication gate selector polynomial
  pub qm:          Poly,
  /// Q_O(X): output wire selector polynomial
  pub qo:          Poly,
  /// Q_C(X): constant selector polynomial
  pub qc:          Poly,
  /// S_σ1(X): first permutation polynomial
  pub s1:          Poly,
  /// S_σ2(X): second permutation polynomial
  pub s2:          Poly,
  /// S_σ3(X): third permutation polynomial
  pub s3:          Poly,
}
}

Permutation arguments

PLONK handles copy constraint across trace using multiset arguments, also called permutation arguments that essentially proves that set $f=\{f_1,f_2,\dots ,f_n\},g=\{g_1,g_2,\dots ,g_n\}$ are permutation of each other in the domain, i.e. $g_i=f_{\sigma (i)}\forall i\in [1,n]$. For more info on permutation arguments, please check out resources mentioned in references.

$$\prod _{i=0}^n(g_i+i)=\prod _{i=0}^n(f_{\sigma (i)}+\sigma (i))$$

permutation helper creates ${\sigma }_i$ polynomials for $i=\{1,2,3\}$.

• creates a execution trace of n rows for each constraint, and 3 columns representing each wires in a gate: LEFT, RIGHT, OUTPUT
• parses each constraint and create a map of variable usage across constraints in tuples of rows and columns.
  • In our example: 3 distinct variable exist, then map of variable usage is {'x': [(1, LEFT), (2, LEFT), (2, RIGHT), (3, RIGHT)], 'x2': [(2, OUTPUT), (3, LEFT)], 'out': [(3, OUTPUT)]}
• to create $g_i$, and $f_i$, shifts each variable usage by 1 to right, i.e. variable at $x_i=x_{i+1}$.
  • for example: x's usage gets shifted 1 to right, new one becomes: {'x': [(3, RIGHT), (1, LEFT), (2, LEFT), (2, RIGHT)]}.
  • This ensures that variables x is copied from $x_i$ to $x_{i+1}$

#![allow(unused)]
fn main() {
/// `Program` represents constraints used while defining the arithmetic on the inputs
/// and group order of primitive roots of unity in the field.
#[derive(Debug, PartialEq)]
pub struct Program<'a> {
  /// `constraints` defined during arithmetic evaluation on inputs in the circuit
  constraints: Vec<WireCoeffs<'a>>,
  /// order of multiplicative group formed by primitive roots of unity in the scalar field
  group_order: usize,
}
}

References

• 0xPARC's plonkathon compiler
• PLONK by hand: Part 2
• on PLONK and PLOOKUP
• Plonk's permutation, the definitive explanation

Curves

Everything in ronkathon (and much of modern day cryptography) works with elliptic curves $E$ as primitives. Simply put, an elliptic curve is a curve defined by the equation $y^2=x^3+ax+b$ where $a$ and $b$ are constants that define the curve. When working over a finite field so that $x,ya,b\in {\mathbb{F}}_q$, we put $E({\mathbb{F}}_q)$ to denote the set of points on the curve over the field ${\mathbb{F}}_q$. It turns out that the set of points $E({\mathbb{F}}_q)$ forms a group under a certain operation called point addition. This group, in at least certain cases, is discrete logarithm hard, which is the basis for much of modern day cryptography.

Curve Group and Pluto Curve

For the sake of ronkathon, we use a specific curve which we affectionately call the "Pluto Curve." Our equation is: $$y^2=x^3+3$$ and we work with the field $F_p$ and $F_{p^2}$ where $p=101$. Predominantly, we use the extension $F_{p^2}$ since we need this for the Tate pairing operation. We refer to $F_{101}$ as the PlutoBaseField and $F_{101^2}$ as the PlutoBaseFieldExtension within ronkathon. From which, we also use the terminology of PlutoCurve to refer to $E(F_{101})$ and PlutoExtendedCurve to refer to $E(F_{101^2})$.

We also define a CurveGroup, an extension of FiniteGroup trait representing the group law of the curve.

Type B curve and type 1 pairing

Investigating our curve and choice of field, we find that the curve is Type B since:

• It is of the form $y^2=x^3+b$;
• $p=101\equiv 2\mathrm{mod}3$; It follows that $E({\mathbb{F}}_{101})$ is supersingular which implies that the PlutoCurve has order (number of points) $n=101+1=102$ and PlutoExtendedCurve has order $n^2=102^2=10404$. Finally, the embedding degree of the curve is $k=2$.
• This curve has a 17-torsion subgroup calculated as largest prime factor of order of curve 102 = 17.2.3.

Since, the curve is supersingular, this allows us to define the type-1 Tate pairing $e:G_1\times G_2\to F_{p^2}^{\ast }$ in a convenient manner, where both $G_1,G_2\in {\mathcal{G}}_1$, i.e. the base field subgroup of r-torsion subgroup.

In particular, we can pick ${\mathbb{G}}_1$ to be the $r$-torsion subgroup of PlutoCurve where $r=17$ is the scalar field of the curve. Note that $r=17$ is valid since $17\nmid 101-1$ and $17\mid 101^2-1$ (Balasubramanian-Koblitz theorem).

In this case, we pick $G=Z_{17}$ and define our pairing as: $$e(P,Q)=f(P,\Psi (Q){)}^{(p^2-1)/r}$$ where $f$ is the Tate pairing and $\Psi$ is the map $\Psi (x,y)=(\zeta x,y)$ where $\zeta$ is a primitive cube root of unity. This is due to the fact that $\Psi$ is the distortion map that maps a factor of $E(F_{101^2})[17]\cong Z_{17}\times Z_{17}$ (which is the $17$-torsion group) to the other.

Pairing and Miller's algorithm

Let's dive a little bit deeper into divisors, and miller's algorithm.

Divisors essentially are just a way to represent zeroes and poles of a rational function. We are interested in divisors of functions evaluated on Elliptic curves, i.e. $\text{div}f={\sum }_{P\in E}{n}_P(P)$.

For example: let's take a function $f=x^3-8$ with $x\in \mathbb{C}$, it's divisor is written as $(f)$ and it has a zero of order 3 at $x=2$ and a pole of order 3 at $x=\infty$, thus, $(f)=3(2)-3(\infty )$.

For an elliptic curve, a line usually intersects the curve at 3 points $P,Q,R=(P+Q)$, then the divisor is written as $(l)=(P)+(Q)+(R)-3(O)$. Note all of these divisors are degree-zero divisors as sum of their multiplicities is 0. There's another concept called support of divisor = $\text{supp}(D)=\{P\in E:n_P\ne 0\}$.

Now, we have most of the things we need to represent tate pairing:

$$e(P,Q)=f_P(D_Q)$$

where $f_P$ is a rational function with $(f_P)=r(P)-r(O)$ and $D_Q$ is the divisor equivalent to $(D_Q)\sim (Q)-(O)$.

Miller's algorithm

$f_{r,P}$ can be calculated as $f_{r-1,P}\cdot \frac{l_{[r-1]P,P}}{v_{rP}}$ where $l_{[m]P,P}$ is the line from $[m]P$ and $P$, and $v[m]P$ is the vertical line going from $m[P],-[m]P$. Both of these lines are used in chord-and-tangent rule in Elliptic curve group addition law.

Usual naive way is impractical on where $r\sim 2^{160}$, and thus, for practical pairings, Miller's algorithm is used that has $O(\log r)$ time complexity, and uses an algorithm similar to double-and-add algorithm.

Helpful Definitions

Here are a few related definitions that might be helpful to understand the curve and the pairing.

roots of unity

the $rth$ root of unity in $F_p$ is some number $h$ such that $h^r\equiv 1$, For example in our field scaler field $F_{101}$ the $4th$ roots of unity are $\{1,10,91,100\}$.

$r$-torsion

$r$-torsion points are points $P\in E(K)|rP=O$ for some point $P$ so that $P$ has order $r$ or is a factor of $r$. The set of r-torsion points in $E(K)$ is denoted $E(K)[r]$. If $\bar{K}$ is the algebraic closure of $K$ then the number of r-torsion points in $E(K)$ is the number of points in $E(\bar{K})[r]=r^2$.

• Security note: If $r$ and $q$ are not co-prime then the discrete log is solvable in linear time with something called an anomaly attack.

Frobenius endomorphism

Curve endomorphisms are maps that take points in one a curve subgroup and map them to themselves. An example is point addition and point doubling. The Frobenius endomorphism denoted $\Phi$ takes points in $P\in E(F_q)$ and maps them $\Phi (P)=(X^q,Y^q)$ .

For higher powers of the map you write ${\Phi }^k$ .

Trace Map

This then allows us to define the trace map which takes points in $E(F_{q^k})$ and maps them to $E(F_q)$

$$tr(P)=P+\Phi (P)+...+{\Phi }^{k-1}(P)$$

Since $k=2$ in our parameters we get $tr(P)=P+\Phi (P)$.

Trace Zero Subgroup: The set of points of trace zero $G=\{P|trP=O\}$ is a cyclic group of order $r$, and every $P\in G$ satisfies $\Phi (P)=qP$ .

Quadratic Non Residue

A Quadratic Non-residue is a number that, cannot be expressed as a square of any other number. In other words, for a given modulus $n$, a number $b$ is a quadratic non-residue if there is no number a satisfying the congruence $a^2\equiv b$ (mod n).

An example of quadratic non-residues would be the number 2 in modulo 3, 4, or 5. In these cases, there is no integer that we can square and then divide by the given modulus to get a remainder of 2.

References

Note that most of these are gross over-simplification of actual concepts and we advise you to refer to these references for further clarifications.

• Ben Lynn's Thesis
• Craig Costello's PairingsForBeginners
• Pairings in depth

Digital Signature Algorithms (DSA)

What are digital signatures?

Like its name, Digital Signatures are digital analogs of physical signatures. For example, when you want to write a cheque you have to "sign" it for authentication purposes. But think about how you would do the same over the internet. Here is where Digital Signatures come into the picture.

Digital Signatures have the following properties:

1. Authenticity: Just like physical signatures, digital signatures provide a way to verify the identity of a signer.
2. Integrity: Digital signatures provide a mechanism to detect unauthorized modification to a message.
3. Non-repudiation: Digital signatures have a nice property that once a signer signs a message, they cannot deny having done so.

How does a digital signature scheme look like?

Digital signature schemes consists of three algorithms $\text{Gen, Sign, Verify}$, such that:

1. The key generation algorithm, $\text{Gen}$ which takes in the security parameter $n$ and outputs public key, $\text{pk}$ and private key, $\text{sk}$.
2. The signing algorithm $\text{Sign}$ takes as input the keys and a message and outputs a signature.
3. The verification algorithm $\text{Verify}$, takes as input the public key, a message, and a signature. It outputs bit 1 if the signature is valid for the given message and public key, otherwise 0.

How is a digital signature scheme used?

To explain how digital signature schemes are used, let's take the example of two people, Bobby and Alex. Bobby is the one whose signature is required, so Bobby will run the $\text{Gen(n)}$ algorithm to obtain, $\text{pk, sk}$. Then, the public key, $\text{pk}$, is publicized as belonging to Bobby. This not only provides authentication but also ensures non-repudiation. This one of the critical parts of a secure digital signature scheme. You can read more on this here: Public key infrastructure

Now when Alex sends a message(document, contract, etc.), $m$, for Bobby to sign, they compute the signature, $s$ as, $s\leftarrow \text{Sign(sk,m)}$ and sents $s$ to Alex or any other party who wants to take a look. Now, any party who wants to see if Bobby signed the document or not, applies the verification algorithm using the public key as $\text{Verify(pk,m,s)}$. Thus Alex or any other party can be sure of the authenicity of the signature as well as the integrity of the message.

When is a signature scheme said to be secure?

A digital signature scheme is said to be secure if an adversary is unable to generate a forgery, that is, a message (not previously signed) and a valid signature for a fixed public key, in any case.

Examples of digital signature scheme

1. Elliptic Curve Digital Signature Scheme(ECDSA)
2. Edwards-Curve Digital Signature Scheme(EdDSA)

References

1. "Introduction to Modern Cryptography" by Jonathan Katz and Yehuda Lindell
2. Digital Signatures

Tiny RSA

RSA was one of the first asymmetric cryptographic primitives in which the key used for encryption is different from the key used for decryption. The security of RSA is based on the difficulty of factoring large integers.

Key Generation

1. Consider two large prime numbers $p$ and $q$.
2. Calculate $n=p\times q$
3. Calculate $\varphi (n)=(p-1)\times (q-1)$
4. Choose $e$ such that $1<e<\varphi (n)$ and $e$ is coprime to $\varphi (n)$, or in other words $gcd(e,\varphi (n))=1$
5. Calculate $d$ such that $d\times e\equiv 1\mathrm{mod}\varphi (n)$

Keys

Private Key = $(d,n)$ Public Key = $(e,n)$

Encryption

• $c=m^e\mathrm{mod}n$

Decryption

• $m=c^d\mathrm{mod}n$

See the examples in the tests.rs file

Security Assumptions

The security of RSA relies on the assumption that it is computationally infeasible to factor large composite numbers into their prime factors, known as the factoring assumption. This difficulty underpins the RSA problem, which involves computing eth roots modulo n without the private key.

Symmetric Encryption algorithms

Symmetric encryption algorithms are cryptographic algorithms that uses same key for encryption and decryption.

Block Ciphers

TODO

Stream ciphers

stream ciphers are symmetric encryption cryptography primitives that works on digits, often bits, rather than fixed-size blocks as in block-ciphers.

$$\begin{array}{r}\mathrm{Enc}(s,m)=c=G(s)\oplus m\\ \mathrm{Dec}(s,c)=m=c\oplus G(s)\end{array}$$

• Plaintext digits can be of any size, as cipher works on bits, i.e. $c,m\in \{0,1{\}}^L$
• $G$ is a PRG that generatoes Keystream which is a pseudorandom digit stream that is combined with plaintext to obtain ciphertext.
• Keystream is generated using a seed value using shift registers.
• Seed is the key value required for decrypting ciphertext.
• Can be approximated as one-time pad (OTP), where keystream is used only once.
• Keystream has to be updated for every new plaintext bit encrypted. Updation of keystream can depend on plaintext or can happen independent of it.

flowchart LR
k[Key]-->ksg["Key Stream Generator"]
ksg--s_i-->xor
x["Plaintext (x_i)"]:::hiddenBorder-->xor["⊕"]
xor-->y_i
y_i["Ciphertext (y_i)"]-.->ksg

Now, encryption in stream ciphers is just XOR operation, i.e. $y_i=x_i\oplus s_i$. Due to this, encryption and decrpytion is the same function which. Then, comes the major question:

Implementations

• ChaCha stream cipher

AES encryption

Advanced Encryption Standard (AES) is a symmetric-key algorithm and is a variant of the Rijndael (pronounced 'rain-dull') block cipher. AES supersedes the Data Encryption Standard (DES).

Overview

AES supports a block size of 128 bits, and three different key lengths: 128, 192, and 256 bits. It manipulates bytes instead of individual bits or 64-bit words, and views a 16-byte plaintext as a 2D column-major grid of bytes.

AES uses Substitution-Permutation Network (SPN) which makes use of two main properties: confusion and diffusion. Confusion means that the input undergoes complex transformations, and diffusion means that these transformations depend equally on all bits of the input.

Unlike DES, it does not use a Feistel network, and most AES calculations are done in a particular finite field.

Algorithm

The core encryption algorithm consists of the following routines:

• KeyExpansion
• AddRoundKey
• SubBytes
• ShiftRows
• MixColumns

For decryption, we take the inverses of these following routines:

• InvSubBytes
• InvShiftRows
• InvMixColumns

Note that we do not need the inverses of KeyExpansion or AddRoundKey, since for decryption we're simply using the round keys from the last to the first, and AddRoundKey is its own inverse.

Encryption

Encryption consists of rounds of the above routines, with the number of rounds being determined by the size of the key. Keys of length 128/192/256 bits require 10/12/14 rounds respectively.

Round 1 is always just AddRoundKey. For rounds 2 to N-1, the algorithm uses a mix of SubBytes, ShiftRows, MixColumns, and AddRoundKey, and the last round is the same except without MixColumns.

KeyExpansion

The KeyExpansion algorithm takes a 128/192/156-bit key and turns it into 11/13/15 round keys respectively of 16 bytes each. The main trick to key expansion is the fact that if 1 bit of the encryption key is changed, it should affect the round keys for several rounds.

Using different keys for each round protects against slide attacks.

To generate more round keys out of the original key, we do a series of word rotation and/or substitution XOR'd with round constants, depending on the round number that we are in.

For round i, if i is a multiple of the length of the key (in words):

#![allow(unused)]
fn main() {
    Self::rotate_word(&mut last);
    word = (u32::from_le_bytes(Self::sub_word(last))
      ^ u32::from_le_bytes(ROUND_CONSTANTS[(i / key_len) - 1]))
    .to_le_bytes();
}

if i + 4 is a multiple of 8:

#![allow(unused)]
fn main() {
    word = Self::sub_word(last)
}

The final step is always to XOR previous round's round key with the (i - key_len)-th round key:

#![allow(unused)]
fn main() {
      let round_key = expanded_key[i - key_len]
        .iter()
        .zip(last.iter())
        .map(|(w, l)| w ^ l)
        .collect_vec()
        .try_into()
        .unwrap();
}

AddRoundKey

XORs a round key to the internal state.

SubBytes

Substitutes each byte in the State with another byte according to a substitution box.

ShiftRow

Do a left shift i-th row of i positions, for i ranging from 0 to 3, eg. Row 0: no shift occurs, row 1: a left shift of 1 position occurs.

MixColumns

Each column of bytes is treated as a 4-term polynomial, multiplied modulo x^4 + 1 with a fixed polynomial a(x) = 3x^3 + x^2 + x + 2. This is done using matrix multiplication.

More details can be found here.

Decryption

For decryption, we use the inverses of some of the above routines to decrypt a ciphertext. To reiterate, we do not need the inverses of KeyExpansion or AddRoundKey, since for decryption we're simply using the round keys from the last to the first, and AddRoundKey is its own inverse.

InvSubBytes

Substitutes each byte in the State with another byte according to a substitution box. Note that the only difference here is that the substitution box used in decryption is derived differently from the version used in encryption.

InvShiftRows

Do a right shift i-th row of i positions, for i ranging from 0 to 3, eg. Row 0: no shift occurs, row 1: a right shift of 1 position occurs.

InvMixColumns

Each column of bytes is treated as a 4-term polynomial, multiplied modulo x^4 + 1 with the inverse of the fixed polynomial a(x) = 3x^3 + x^2 + x + 2 found in the MixColumns step. The inverse of a(x) is a^-1(x) = 11x^3 + 13x^2 + 9x + 14. This multiplication is done using matrix multiplication.

More details can be found here.

Substitution Box

A substitution box is a basic component of symmetric key algorithms performs substitution. It is used to obscure the relationship the key and the ciphertext as part of the confusion property.

During substitution, a byte is interpreted as a polynomial and mapped to its multiplicative inverse in Rijndael's finite field: GF(2^8) = GF(2)[x]/(x^8 + x^4 + x^3 + x + 1).

The inverse is then transformed using an affine transformation which is the sum of multiple rotations of the byte as a vector, where addition is the XOR operation. The result is an 8-bit output array which is used to substitute the original byte.

Security

Fundamentally, AES is secure because all output bits depend on all input bits in some complex, pseudorandom way. The biggest threat to block ciphers is in their modes of operation, not their core algorithms.

Practical implementations

In production-level AES code, fast AES software uses special techniques called table-based implementations which replaces the SubBytes-ShiftRows-MixColumns sequence with a combination of XORs and lookups in hardcoded tables loaded in memory during execution time.

References

• FIPS197
• Serious Cryptography - A Practical Introduction to Modern Cryptography

ChaCha Encryption

• ChaCha's core is a permutation $P$ that operates on 512-bit strings
• operates on ARX based design: add, rotate, xor. all of these operations are done 32-bit integers
• $P$ is supposed to be secure instantiation of random permutation and constructions based on $P$ are analysed in random-permutation model.
• using permutation $P$, a pseudorandom function $F$ is constructed that takes a 256 bit key and 128-bit input to 512-bit output with a 128-bit constant.

$$F_k(x)\stackrel{def}{=}P(\mathrm{const}\parallel k\parallel x)⊞\mathrm{const}\parallel k\parallel x$$

Then, chacha stream cipher's internal state is defined using $F$ with a 256-bit seed $s$ and 64-bit initialisation vector $IV$ and 64-bit nonce that is used only once for a seed. Often defined as a 4x4 matrix with each cell containing 4 bytes:

Let's define what happens inside $F$, it runs a quarter round that takes as input 4 4-byte input and apply constant time ARX operations:

a += b; d ^= a; d <<<= 16;
c += d; b ^= c; b <<<= 12;
a += b; d ^= a; d <<<= 8;
c += d; b ^= c; b <<<= 7;

quarter round is run 4 times, for each column and 4 times for each diagonal. ChaCha added diagonal rounds from row rounds in Salsa for better implementation in software. Quarter round by itself, is an invertible transformation, to prevent this, ChaCha adds initial state back to the quarter-round outputs.

This completes 1 round of block scrambling and as implied in the name, ChaCha20 does this for 20 similar rounds. ChaCha family proposes different variants with different rounds, namely ChaCha8, ChaCha12.

Nonce can be increased to 96 bits, by using 3 nonce cells. XChaCha takes this a step further and allows for 192-bit nonces.

Reason for constants:

• prevents zero block during cipher scrambling
• attacker can only control 25% of the block, when given access to counter as nonce as well.

During initial round, counters are initialised to 0, and for next rounds, increase the counter as 64-bit little-endian integer and scramble the block again. Thus, ChaCha can encrypt a maximum of $2^{64}$ 64-byte message. This is so huge, that we'll never ever require to transmit this many amount of data. IETF variant of ChaCha only has one cell of nonce, i.e. 32 bits, and thus, can encrypt a message of $2^{32}$ 64-byte length, i.e. 256 GB.

DES encryption

DES is a symmetric encryption algorithm based on Feistel cipher. It has following properties:

• Message block size is 64-bits.
• Key size is 64 bytes, where every 8th bit is parity bits, so realized key size is 56 bits.
• Encryption algorithm is based on Feistel cipher containing 16 identical rounds with new subkey for each round derived using Key Schedule algorithm.
• Encryption algorithm divides 64 bit message into two halves of 32 bits and then, acted upon by round functions.
• Due to structure of Feistel ciphers, encryption and decryption algorithms, only difference in decryption algorithm being subkeys are reversed.
• Since, key size is 56-bits, it's prone to brute force attacks, where exhaustive key search is done to calculate the key for known plaintext.

Implementation details

• limbs of 8 bits are used to denote different types, i.e. 64, 56, 48, 32 in the encryption function.
• all data is represented in big-endian order.
• Refer to tests for detailed examples and attack vectors.
  • Known-plaintext attack: brute force approach using exhaustive key search on the complete key space, i.e $[0,1<<2^{56}-1]$.
  • Weak key attack: 4 weak keys are possible where encryption and decryption are same. This is only possible when all round subkeys are identical.
  • bit complement: DES has a nice property where $y=EN{C}_k(x)$ and $y^{\prime }=EN{C}_{k^{\prime }}(x^{\prime })$

Permutation

Shuffles the bits according to permutation table based on indexes. Let's understand this with an example from Simplified DES:

Let a 10-bit key be denoted as: $K=(k_1,k_2,\dots ,k_{10})$, and a permutation table defined as:

$$\begin{array}{cccccccccc}3& 5& 2& 7& 4& 10& 1& 9& 8& 6\end{array}$$

Applying permutation $P$ to key $K$, $P(K)=(k_3,k_5,k_2,k_7,k_4,k_{10},k_1,k_9,k_8,k_6)$.

[!NOTE] Permutation table length can vary according to the bits required in the output. Let's say, if $P=[3,5]$, then output will be only 2 elements of the key, i.e. $k_3,k_5$. This is used throughout DES to reduce or increase data lengths.

Substitution

DES uses substitution in the form of S-boxes in it's encryption algorithm. Substitution is necessary, as it provides non-linearity in the cipher. Without non-linearity, DES's encryption function could be represented as a set of linear equations on the secret key variable.

DES performs substitution on 6-bit data and gives 4-bit data. It's implemented as a lookup table, where the row and column from the input data = $(100110{)}_2$ is read as:

• row: $(6,1)$ bits, i.e. 6th and 1st bit = $(10{)}_2=2$
• column: $(5,4,3,2)$ bits = $(0011{)}_2=3$

Thus, input data $38$ represents 3rd row, 4th column in the $4\times 16$ permutation lookup table.

Key schedule algorithm

derives 16 48-bit subkeys, 1 for each round.

• Permutation choice-1: drops every 8th bit and permutes bits
• 56-bit key is divided into two 28-bit halves.
• left shift is applied to both halves depending on the key schedule round.
• Permutation choice-2 is applied reducing 56-bit key to 48-bit subkey.
• repeated for 16 rounds

flowchart TB
Key["Key 64-bit"]-->PC1
PC1[PC-1]-->LS1[<<<]
PC1-->LS2[<<<]
subgraph one [16 rounds]
LS1--->LS3[<<<]
LS1-->PC2[PC-2]
LS2-->PC2
LS2--->LS4[<<<]
LS4-->PC22[PC-2]
LS3-..->a:::hidden
LS3-->PC22
LS4-..->b:::hidden
end
PC2-->SK1[subkey 1]
PC22-->SK2[subkey 2]

classDef hidden display: none;

Encryption algorithm

16 rounds with five functions in the order:

• Initial permutation (IP)
• Feistel function (F): applies substitution and permutation to key
• Mixing: mix two halves together
• Switching: switches left and right halves
• Final Permutation (FP)

Feistel function

Applies substitution, permutation to key which adds to the complexity of the function and increases cryptanalysis difficulty. For substitution, DES uses S-boxes that takes as input 8-bits and output is of length 6-bits.

flowchart TB
key--32 bits-->Exp[Expansion]
Exp--48 bits-->Mix["⊕"]
Sub[Subkey]--48 bits-->Mix
Mix--8-->s1
Mix--8-->s2
Mix--8-->s3
Mix--8-->s4
Mix--8-->s5
Mix--8-->s6
Mix--8-->s7
Mix--8-->s8
s1--6-->P[Permutation]
s2--6-->P
s3--6-->P
s4--6-->P
s5--6-->P
s6--6-->P
s7--6-->P
s8--6-->P
P--32 bits-->Output:::hidden

• Takes as input one half of the key, 32 bits
• use Expansion permutation to increase bits to 48
• Mix the expanded key with round's subkey using xor
• Divides 48-bit output into 8 6-bits elements
• Applies substitution using 8 S-boxes to each element
• Applies permutation using permutation table to get 32-bit output

Modes of Operation

Block ciphers can only do fixed length encryption of bits in a well-defined Block. Modes of operation allows to extend cipher's encryption/decryption algorithms to allow arbitrary length data.

Some operations require Initialisation vector (IV) that must not repeat for subsequent encryption operations, and must be random for some operations. IV is used so that different ciphertext is generated for same plaintext even for a single key. We demonstrate this in our tests.

Appropriate padding has to be performed for some modes, as block ciphers only work of fixed size blocks. Since, most of the ciphers are used with MAC that provides integrity guarantees and prevent Chosen-Ciphertext attacks on the protocol, so, any padding scheme works, most common is PKCS#7 or even null byte padding. Note that, without use of MACs, almost all block ciphers with padding are susceptible to Padding Oracle Attacks and should be handled with utmost care.

Let's go into detail about Block cipher's mode of operation.

Notation

• $C_i$ represents the i-th ciphertext block.
• $En{c}_K$ is the block cipher with key $K$
• $M_i$ represents the i-th plaintext block

Also note that in the figures yellow diamonds represent functions/algorithms and the small rectangle with a blue outline represents blocks of data.

ECB: Electronic codebook (INSECURE)

The encryption operation in ECB can be viewed as,

• It is the simplest mode of encryption but is not secure.
• In this, we independently apply the block cipher on each block of plaintext.
• The algorithm is deterministic, hence it is not secure against Chosen-plaintext Attack(CPA).
• It can be parallelized easily.

CBC: Cipher Block Chaining

The encryption operation in CBC can be viewed as,

• It is a CPA-secure mode of operation.

• The first ciphertext block is called an Initialisation Vector(IV), which is chosen uniformly at random.

• It is defined as, $$C_0=IV,C_i=En{c}_K(C_{i-1}\oplus M_i)$$ where $i$ ranges from 1 to N, the number of blocks required by the plaintext.

• It is sequential in nature, although decryption can be parallelized as inputs to block cipher's encryption is just the ciphertext.

• Chained CBC: A variant of CBC where ciphertext is chained for subsequent encryptions.

  • But it's not CPA secure, as an attacker can distinguish between PRF and uniform random function by choosing appropriate text in second encryption.
  • See the code example that demonstrates this vulnerability!

OFB: output feedback

The encryption operation in OFB can be viewed as,

• IV is chosen uniformly and $Y_0:=IV$, then $Y_i=En{c}_k(Y_{i-1})$ and $C_i=Y_i\oplus M_i$.
• This allows $En{c}_k$ to not be invertible, and can be simply a PRF.
• Due to this, OFB can be used to encrypt plaintext of arbitrary lengths and not have to be multiple of block length.
• Pseudorandom Stream can be preprocessed and then encryption can be really fast.
• It's stateful variant can be used to instantiate stream cipher's synchronised mode of operation and is secure.

CTR: counter mode

The encryption operation in CTR can be viewed as,

• Like OFB, CTR converts a block cipher to a stream cipher. where the keystream, called the Counter Block, is generated using the nonce/IV concatenated with a counter, which is incremented for successive blocks.
• Thus, it can be viewed as unsynchronised stream cipher mode, where $Y_i=En{c}_K(⟨IV\parallel i⟩)$ for the binary string $i=1,2,\dots ,$ and $c_i=y_i\oplus m_i$.
• This again allows $En{c}_K$ to not be invertible and can be instantiated with a Pseudorandom function.
• It can be fully parallelized.

GCM: Galois/Counter Mode

GCM is a block cipher mode of operation that provides both confidentiality and authentication. To provide confidentiality, it uses Counter(CTR) mode for encryption and decryption. To provide authentication, it uses a universal hash function, GHASH. Authentication is provided not only for confidential data but also other associated data.

In this section, we will give an informal overview of GCM mode for 128-bit block cipher. To see the formal definition of the operations of GCM, I recommend reading the original paper. The Galois/Counter Mode of Operation (GCM)

The two operations of GCM are authenticated encryption and authenticated decryption.

Here is a figure that gives a complete overview of the authenticated encryption in GCM.

In the figure, we have taken

• the size of plaintext is 3 * 128-bit = 384 bits or 48 bytes,
• Additionally Authenticated Data(AAD) is of 2 * 128-bit = 248 bits or 32 bytes.

Note: The yellow diamonds represent functions/algorithms, the small rectangle with a blue outline represents 128-bit blocks. Also,

• Enc(K): The encryption operation of the cipher used, for example AES, under the key K.
• incr: The increment function, which treats the rightmost 32-bit of the block as an unsigned integer and increments it by 1.

If you look at the figure carefully, you will notice that the GCM mode is composed of two main parts:

• Encryption: This part is the same as the CTR mode of operation, with minor changes to the counter block.
• Authentication: In this part, we generate an authentication tag for the ciphertext and some additional data, which we refer to as Additionally Authenticated Data(AAD).

The counter block is the same as in CTR mode. In general, it can be thought of as a 96-bit nonce value followed by a 32-bit counter value.

The tag is generated by XOR of:

1. Hash of ciphertext and AAD, using GHASH algorithm
2. Encryption of Counter block 0.

GHASH

The GHASH algorithm can be viewed as a series of ADD and MULTIPLY in $GF(2^{128})$. Mathematically put the basic operation of GHASH is,

$$X_i=\{\begin{array}{ll}0& i=0\\ (X_{i-1}\oplus B_i)\ast H& \text{otherwise}\end{array}$$

$B_i$ represents blocks of AAD followed by blocks of ciphertext followed by a special length block. The length block consists of 64-bit lengths(in bits) of AAD and ciphertext. $H$ called the hash key, is the encryption of 128-bit of zeros using the chosen cipher and key.

The interesting thing to note here is that the multiplication($\ast$) and addition($\oplus$) are operations of the Galois(finite) field of order $2^{128}$. A brief summary of finite field arithmetic,

• The elements of the field are represented as polynomials. Each bit of the 128-bit block represents coefficients of a polynomial of degree strictly less than 128.
• Addition in a finite field is equivalent to bitwise XOR.
• Multiplication in a finite field is the multiplication of corresponding polynomials modulo an irreducible reducing polynomial.

In GCM the reducing polynomial is $f=1+x+x^2+x^7+x^{128}$

If you want to read about Finite Field, the Wikipedia article on Finite Field Arithmetic is pretty good!

The authenticated decryption operation is identical to authenticated encryption, except the tag is generated before the decryption.

Nonce Reuse Attack

In all modes of operation discussed above, the Initialisation Vector(nonce) should be used only once. In case where the nonce is reused, we will be able to obtain the XOR of plaintexts. So, if an adversary has knowledge of one of plaintexts, like Known-plaintext attacks, they will be able to obtain the other plaintext.

Let's look that this in action using GCM mode.

Consider the scenario, where the adversary has knowledge of a plaintext, $m_1$ and its corresponding ciphertext, say $c_1=GC{M}_K(m_1)$ , where $K$ is some key.

Now if the adversary intercepts another ciphertext, say $c_2$, encrypted using the same key $K$ and same nonce. Since GCM (and CTR) is like a stream cipher, where ciphertext is obtained by XOR of keystream and the plaintext. So, $c_1=r_1\oplus m_1$ and $c_2=r_2\oplus m_2$ , where $r_1$ , $r_2$ are some pseudorandom keystreams.

But the same key and nonce pair produce the same keystream, thus, $r_1=r_2=r$.

c_1 = r \oplus m_1 \quad \text{and} \quad c_2 = r \oplus m_2 \\ \implies c_1 \oplus m_1 = c_2 \oplus m_2  \\ \implies m_2 = c_1 \oplus c_2 \oplus m_1

So, after some rearrangement we get that message $m_2$ is the XOR of ciphertexts, $c_1$ and $c_2$ and the known plaintext, $m_1$. Since adversary has the knowledge of all the required information, the adversary can obtain the original plaintext upto the length of the $m_1$.

Next Steps

Implement more modes, and subsequent attacks/vulnerabilities:

• CFB
• OFB

References

• Understanding Cryptography by Cristof Paar & Jan Pelzl & Tim Güneysu: Chapter 3, 4
• Introduction to Modern Cryptography: Section 1

Hash Functions

A hash function is a function that take in an input of arbitrary length, and produces a fixed length output. Moreover, a hash function should be deterministic, meaning that the same input should always produce the same output. Also, we require that the output of a hash function should be uniformly distributed over its output space, meaning that every output should be equally likely given any input.

Intuitively, you can imagine the job for a hash function is to take some arbitrary data and produce a unique "identifier" or "fingerprint" for that data. Given that the output space is large enough (and some other conditions are met), we can use hash functions to do this. In effect, every bit of data we care to create an identifier for can be hashed to a unique output value. For instance, we may have a complete library of works of literature, and by hashing the contents of each book, we can create a unique identifier for each book. Common output spaces are 256-bits, meaning that we would have 2^256 possible outputs. To put this in perspective, the number of atoms in the observable universe is estimated to be around 10^80, which is around the magnitude of 2^256. For back of the envelope calculations, we can note that 2^10 is about 1000=10^3, so 2^256 is about 10^77, which is near the estimates of number of atoms in the observable universe.

SHA-2

SHA-2 is a family of hash functions that includes SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, and SHA-512/256. The SHA-2 family of hash functions are widely used and are considered to be secure, though you should not hash secrets directly with SHA-2 (you can use SHA-3 instead). As with many cryptographic primitives, SHA-2 is standardized by NIST. It is used in many different protocols such as TLS, SSL, PGP, and SSH.

The hash function itself is based on the Merkle-Damgard construction, so it reads in blocks of data and processes them in a certain way. The output of the hash function is the hash of the data, which is a fixed length output. In our case, we will be using SHA-256, which produces a 256-bit output.

For more detail on the implementation of SHA-256 see this resource. Also, you can find JavaScript code and a working applet for SHA-256 here. Our implementation can be found in the src/hashes/sha256.rs file with detailed documentation and comments.

Contains implementation of Poseidon hash function by Grassi et al.. It's main feature is that it's an algebraic hash function suitable for usage in arithmetic proof systems like SNARKs, and modularity with respect to choosing different parameters according to the use case.

Uses mix of following computations at each step:

• round constants: predetermined constants added to each element in state.
• non-linear layer: in the form of s-box
• linear layer: use an MDS (maximally distance separable) matrix of dimensions width * width and perform matrix multiplication with state.

Uses the Hades permutation design strategy and thus, it's round function can be divided into two kinds:

• Partial rounds: non-linear layer is only applied to first element of the state
• Full rounds: non-linear layer is applied to all elements

Security of the function depends mainly on:

• Number of full rounds
• Number of partial rounds
• at each round, the exponent in s-box, choice of matrix in linear layer

rounds are applied in a chaining fashion:

• first, half of full rounds are performed
• then, all partial rounds
• then, half of remaining full rounds
• first element in state is returned as hash output

Permutation

Hash function permutation is responsible for blending the elements to remove any symmetrical properties in the input using round functions.

Permutation at each round of Poseidon works as follows:

• For full rounds $R_f$:
  • round constants are added to each element in state
  • s-box is applied, i.e. each element is raised to power of alpha
  • elements are mixed using linear layer by matrix multiplication with MDS matrix
• For partial rounds $R_p$:
  • round constants are applied same as full rounds
  • s-box is applied only to first element
  • linear layer is applied

Rounds constants add external information to the state and break any symmetrical and structural properties in the input. Poseidon uses Grain LFSR to generate round constants.

S-Boxes imparts non-linearity in the input data. Non-linearity prevents linear attacks which aim to exploit linear relation between round operations. Poseidon uses power of elements, generally $x^3,x^5$, calculated as minimum value such that $\gcd (\alpha ,p-1)=1$.

MDS (Maximally distance separable) matrix are uses in the linear layer of the round. Its main use is to mix the elements together such that any changes made in the non-linear layer are spread throughout the state. Maximally distance separable refers to matrices such that no two rows are linear dependent to each other. This maximises the input differences across the hash state.

Sponge API

Sponge allow to take as input, data of arbitrary size and produce variable length output.

Each hash functions' state is divided into two sections:

• rate: rate at which new elements are absorbed by the sponge
• capacity: remaining elements in sponge state.

Sponge behavior, based on Sponge metaphor which can be explained by following functions:

• Absorb: absorbs new field elements ${\mathbb{F}}_p$ into sponge state.
  • For example: if sponge width is 10 units and sponge rate is 3, then if a 15 unit input is entered, its divided into 5 chunks of 3 units and added to sponge state.
  • After each chunk addition, permutation is performed, until all chunks are absorbed.
• Squeeze: after the absorption, hash's output is returned using squeezing of sponge state.
  • For example: for a sponge with width of 10 units and rate of 3, if hash output of 25 units is required, then:
  • width number of elements are squeezed out of sponge state at each iteration.
  • permutation is performed until required number of elements are squeezed out.

[!NOTE] Only rate section is acted upon in absorb and squeeze of Sponge API, and capacity section is left untouched. Absorption of new elements and squeeze output is taken from rate section. This allows permutation to mix the elements thoroughly.

Absorption operation can be different for different hash functions. For example: Keccak uses xor to absorb new elements. Since Poseidon is an algebraic hash function and based on finite fields, it uses addition of field elements.

Example

First, we need to generate round constants which will be used in poseidon parameters. Poseidon requires following parameters for initialisation:

• ${\mathbb{F}}_p$: finite field
• WIDTH: width of the state of the hash
• ALPHA: used in s-box layer
• NUM_P: number of partial rounds
• NUM_F: number of full rounds
• rc: round constants used in round constant layer of a round
• mds: matrix used in linear layer of a round

This can be generated using sage file provided at project's core. Run following command to generate a constants file:

• Usage: <script> <field> <s_box> <field_size> <num_cells> <alpha> <security_level> <modulus_hex>
• field = 1 for GF(p), 0 for GF(p^k)
• s_box = 0 for x^alpha, s_box = 1 for x^(-1)

sage poseidon_constants.sage 1 0 7 16 3 10 0x65

Here's an example to use Poseidon struct for hashing input of length WIDTH. Note that input is padded with extra zeroes if length is not equal to width.

#![allow(unused)]
fn main() {
use ronkathon::field::prime::PlutoBaseField; // can be any field that implements FiniteField trait

const WIDTH: usize = 10;
const ALPHA: usize = 5;
const NUM_P: usize = 16;
const NUM_F: usize = 8;

// load round constants and mds matrix
let (rc, mds) = load_constants::<PlutoBaseField>();

// create a poseidon hash object with empty state
let mut poseidon = Poseidon::<PlutoBaseField>::new(WIDTH, ALPHA, NUM_P, NUM_F, rc, mds);

// create any input
let input = std::iter::repeat(PlutoBaseField::ZERO).take(WIDTH).collect();

// perform hash operation
let res = poseidon.hash(input);

println!("{:?}", res);
}

Another example using Sponge API for arbitrary length element hashing. Simplex sponge supports arbitrary length absorption with arbitrary length squeeze.

#![allow(unused)]
fn main() {
use rand::rng;
use ronathon::field::prime::PlutoBaseField;

let size = rng.gen::<u32>();

// create any state
let input = std::iter::repeat(PlutoBaseField::ONE).take(size).collect();

let (rc, mds) = load_constants::<PlutoBaseField>();

let mut pluto_poseidon_sponge = PoseidonSponge::new(WIDTH, ALPHA, NUM_P, NUM_F, rate, rc, mds)

let absorb_res = pluto_poseidon_sponge.absorb(&input);
assert!(absorb_res.is_ok());

let pluto_result = pluto_poseidon_sponge.squeeze(squeeze_size);
assert!(pluto_result.is_ok());
}

More info and examples can be found in tests.

Next steps

• Grain LFSR for round constants generation
• Duplex sponge
• Possible attacks using tests

References

• Poseidon by Grassi et al.
• Poseidon Journal
• Sponge API

HMAC (Hash-based Message Authentication Code)

Overview

HMAC is a cryptographic primitive for providing message integrity and authenticity using a cryptographic hash function in combination with a secret key. It ensures that both the data (message) and its origin (authenticity) are verified.

Components

• Hash Function: A one-way function that produces a fixed-size output (hash) from an input (message). Common hash functions include SHA-256, SHA-1, and MD5.
• Secret Key: A private key used to generate and verify the HMAC. It should be kept confidential.
• Message: The data or payload that is being protected by HMAC.

How HMAC Works

1. Key Padding: If the secret key is shorter than the block size of the hash function, it is padded. If it is longer, it is hashed to reduce its length.
2. Inner Hash Calculation: Combine the padded key with the message and compute the hash. This step involves XORing the key with a specific value and then hashing the result concatenated with the message.
3. Outer Hash Calculation: Combine the padded key with a second specific value, hash the result concatenated with the inner hash, and produce the final HMAC.

More specifically, HMAC is defined as: $${\text{HMAC}}_K(M)=\text{H}\left((K^{\prime }\oplus \text{opad})\Vert \text{H}((K^{\prime }\oplus \text{ipad})\Vert \text{M}\right)$$ where:

• $H$ is a cryptographic hash function.
• $M$ is the message.
• $K$ is the secret key.
• $K^{\prime }$ is a block-sized key derived from the secret key $K$.
• $\text{opad}$ is the block-sized outer padding.
• $\text{ipad}$ is the block-sized inner padding.
• $\Vert$ denotes concatenation.

Some notes on the KZG proof construction:

Lets start simple with a finite field and work up to creating two elliptic curve groups that have a pairing or bilinear map (more on that later). First lets pick a finite field of prime order $p$, we pick $p=101$ since it is small and we are able to follow along plonk-by-hand. In general large primes are good but we will use a small one just for the sake of example. Next lets pick an elliptic curve $y^2=x^3+3$, there are some heuristics to curves that we encourage you to learn more about if you like but you can also black box and know that this is a good curve. So now we have two algebraic structures:

• finite field $F_{101}$
• curve $y^2=x^3+3$ Initially this elliptic curve is just a continuous squiggle, which isn't the most useful. But we can make it discrete by constraining it's points to reside in the field. Now it doesn't look like the squiggle we know and love but instead a lattice (you can see here by switching from real numbers to finite fields ).

Now we have a set of discrete points on the curve over the finite field that form a group, a group has a single operation called the group operation, it is perhaps more abstract than a field. The group operation on this set of curve points is point addition which we all know and love with the squiggly lines, intersections and reflections. From this group operation we can create point doubling, and as a result, scalar multiplication (how many times do we double a point) as handy abstractions over the single group operation.

To review we have a curve group call it $E1$ and the base field $F_{101}$ Elements in the curve group are points (pairs of integers) that lie in the field $F_{101}$.

Now to create a pairing friendly curve we first must find the curve groups order. The order is how many times do we double the generator to get the generator again, the reason we can do this is because our group is cyclic. Now if our base field $F_{101}$ is of prime order, then any point in the curve group is a generator. So in practice you can pick a point and double it until you get back to itself (remember to check the inverse!). This defines the scalar field $F_r$ where $r$ is the order. In our case this is $17$. Once we have have this we can computer the embedding degree. The embedding degree is the smallest number $k$ such that $r|p^k-1$ where $r$ is the order of the curve: $17$ For us this is $2$, we can check that 17 divides $101^2-1$ as $10200/17=600$ ✅. So now we have an embedding degree of our curve.

The next step is to construct a field extension from the first field such that $f_{p^2}$ is a field extension of $f_p$, we extend with $x^2+2$ which is irreducible in $F_{101}$ The elements of the extension field are two degree polynomials where the coefficients are in $F_{101}$ Now we can construct pairing friendly curve over the field extension and get a generator point for the second curve: $g2=(31,36x)$ Our second curve group now E2, is over the same curve but now over the field extension. It's points are now represented by two degree polynomials (because our embedding degree is two), not integers. We now have two pairing friendly groups $E1$ and $E2$ and generators for both of them.

The next step is to construct the structured reference string SRS with g1 and g2. The structured reference string is generated by multiplying the generator points by some randomness $\{S^i\}$, the SRS needs to be a vector of length $t$ where $t$ is the number of constraints in the proof. This is same as the degree of the polynomial which we would like to prove knowledge of. KZG Proves an arbitrary polynomial. Plonk can be used to represent some computation as a polynomial.

Commit to a polynomial using the g1_SRS: This is done by multiplying the polynomial coefficients by the g1_SRS points (scalar multiplication in the curve group) and adding the resulting points to each other to get a single point that represents the commitment call it p_commit.

Opening involves choosing a point to evaluate the polynomial at and dividing the polynomial by .... (need the notes for this). the resulting polynomial is also combined with the g1_SRS to get a new commitment curve point call it q_commit.

Then we do the pairing check.

$e(q_{commit},g2srs[0]-g2\ast point)=e(p_{commit}-g1srs[0]\ast val,g2)$

Resources

• KZG introduction by dankrad

Merkle Trees

What is a Merkle Tree?

Simply put, a Merkle tree is a data structure that acts as a collision-resistant hash function with some interesting properties.

More specifically,

1. A Merkle tree can be viewed as a collision-resistant hash function that takes n inputs and outputs Merkle root hash.
2. A verifier that has only the root hash and any one of the inputs, say $x$, can be convinced that $x$ was actually one of the inputs used to build the Merkle tree using a small-sized proof.

Now let's understand how Merkle Trees works?

Construction of Merkle Tree

Let's say Bob is given $n$ inputs. For our example let's take $n=8$.

To create a Merkle Tree, Bob follows the following steps-

1. In the first step, we hash each of the inputs using a collision-resistant hash function, say $H$.
2. In the next step, we concatenate adjacent hashes and hash it again using $H$. Now we are left with 4 hashes.
3. We repeat the last step until a single hash is left. This final hash is called the Merkle root hash.

Voila!

In summary, the Merkle tree is a tree of hashes built bottom-up from its leaves.

Now that the Merkle tree is built, Bob's friend, Alice, wants to give one of the inputs, say $x_3$. And, Alice wants to be sure that $x_3$ is the same input that Bob used to create the Merkle tree. This is where the Merkle Proof comes into the picture.

Merkle Proof

Let's say that Alice was given the Merkle root hash using a trusted source and/or the root hash was digitally signed. But the data, $x_3$, maybe transferred through an untrusted channel.

Now, Bob can send the Merkle proof, which will be enough to convince Alice that Bob has the same file.

What is a Merkle proof? Merkle proof is a small part of the Merkle tree which along with $x_3$ can be used to recompute the Merkle root hash. The recomputed root hash can be verified with the trusted root hash.

So what part of the tree is included in the Merkle proof?

Remember that our goal is to recompute the hash at root. If you look at the path from $x_3$ to the root, at each level we concatenate the value at the current node with the sibling and hash the resultant. Thus, if we are only given the sibling hashes at each level we could recompute the root hash.

In the image below, the nodes marked in yellow will be part of the Merkle Proof and the red nodes will recomputed during the verification step.

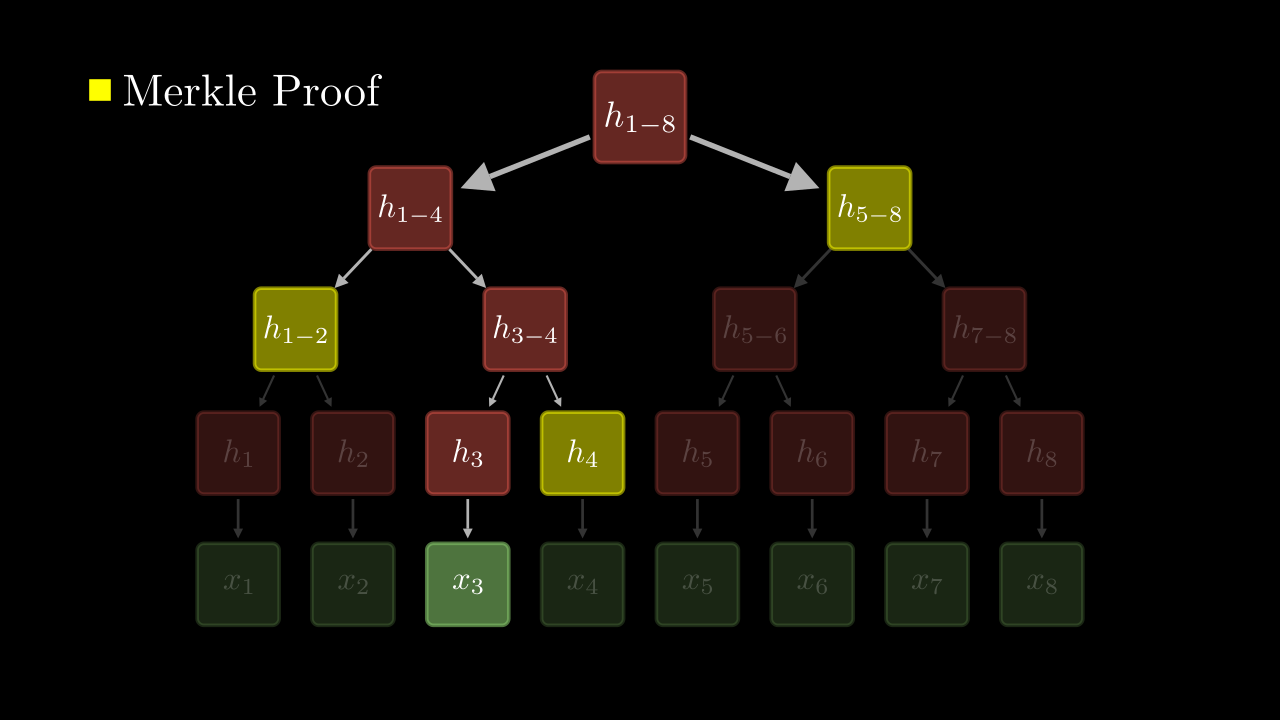
Merkle Proof, which is a set of hashes, may contain additional information about which branch, left or right, each hash value belonged to.

So, Merkle Proof for $x_3$ will look like: {($h_4$, Right), ($h_{1-2}$, Left), ($h_{5-8}$, Right)}

You can see for yourself by running the merkle_tree.rs example in examples folder.

That's it! Now we understand how Merkle Tree is created and what Merkle Proof is.

If you want to read more about Merkle Trees, I highly recommend What is a Merkle Tree? from which this article is based.